CMPS 2120 Week 5 Lecture Notes - Introduction to Sets
resources:
set identities
*************************
* Introduction to Sets *
*************************
A set is a collection of unordered, unique elements.
An *ordered set* is a collection of ordered unique elements.
S ::= {4,23,7} reads "S is defined as the set containing 4, 23, and 7."
S = {1,2,3) reads "S is the set containing 1, 2, and 3.
4 ∈ S, reads "4 is a member of set S." or "4 is in S."
A set may contain sets as members. Let S = {1, {2,3}, {5, {2}}, 7}. S
has 4 members. 2 members are sets, and one of those sets also contains a set.
T ⊆ S reads "T is a subset of S."
Set T is a subset of S if every element of T is in S. Let S={{2,3},1,7}. If
T={(2,3), 1} then T ⊆ S. If U={{2,3}, 5}, U is not a suset of S.
T ⊂ S reads "T is a proper subset of S."
S is a proper subset of T if S is a subset of T and S != T.
Do not confuse subset and set membership operations:
Let S ::= {1,{2,3}, {5,{2}}, 7}.
Then {2,3} ∈ S and {{2,3}} ⊆ S.
Every set is the subset of itself; {2,3} is a subset of {2,3}.
Let S and T be sets. S = T if all the members of S are in T and all the
members of T are in S.
{} = empty set (also called the null set and also denoted by ∅).
The empty set is not the same as *nothing* - it is the set containing nothing.
{} is a subset of every other set.
{} is a subset of {}. (This does not mean that {} is a member of {}.)
The cardinality of set S, denoted by |S|, is the number of distinct elements
in S. Let S={2,3,4,10}. Then |S| = 4. Let S={2,(2),3}. Then |S| = 3.
|{}| = 0. The cardinality of the empty set is zero.
The cardinality of a set that is not finite is infinite; e.g. the set of
natural numbers 0,1,2,3,4,..... is infinite.
Infinite sets are defined by set builder notation: Ex.
To define the set of all integers > 1:
R ::= {x | x is an integer > 1}
Reads:
"R is defined as the set containing all x, such that x is an integer > 1"
POPULAR SETS. SET CONTAINING:
Z = { .... -2, -1, 0, 1, 2, .... } integers
Z+ = {1, 2, .... } positive integers
N = { 0, 1, 2, .... } natural numbers
Q = { p/q | p ∈ Z, q ∈ Z, q != 0} rational numbers
R = { -9, 0, 2/3, pie, e, sqrt(2), etc. } real numbers
The power set of a set S, denoted by P(S),is the set containing all subsets
of S.
For S={2,3,4}, P(S)={{}, {2}, {3}, {4}, {2,3}, {2,4}, {3,4}, {2,3,4}}
|P(S)| = 2^|S|
Given sets A and B, the Cartesian product A x B (reads "A cross B"), is the
set of all possible ordered pairs (a,b), with 'a' ∈ A and 'b' ∈ B.
The Cartesian product A x B x C is the set of all possible ordered 3-tuples
<a,b,c> with 'a' ∈ A, 'b' ∈ B, and 'c' ∈ C. Tuples can also
be enclosed in parentheses: (a,b,c).
|A x B x ... x n| = |A|*|B|* ... * |n|
A x {} = {}
Questions:
Is 2 ∈ {{2}, 2 }? yes
Is 2 ∈ {{2}, 3 }? no
Is {} ∈ { 2, 3 }? no; if yes, the null set would be an explicit member
Is {} ∈ {{}}? yes
Is {} ∈ {}? no
Is {{}} ∈ {{}}? no
Is {5} ∈ {5}? no
Is {5} ⊆ {5}? yes - every set is a subset of itself
Is {{}} ⊆ {{}}? yes - every set is a subset of itself
Is {2,3} ⊂ {2,3}? no - a set is not a proper subset of itself
Is {} ⊆ {}? yes-the null set is a subset of every set, inc. itself
Is {} ⊆ {2,3}? yes-the null set is a subset of every set
Q; If S={{a}, {{a}}, {{a},{{a}}}}, what is |S|?
A: The cardinality of S is 3 (count the commas).
Q: If P(A)=P(B), does A=B?
A: yes-if the power sets are equal then the sets must be
Q: Is {} a power set of a set?
A: no, the smallest power set is {{})
Q: If |S|=7, could S be a power set of another set?
A: no,the cardinality of power sets is 2^n, n>=0
Q: What is A x B x C, for A={2,3}, B={4,5,6} and C={7}?
A: {(2,4,7), (2,5,7), (2,6,7), (3,4,7), (3,5,7), (3,6,7)}
**********************
* Set Operations *
**********************
A ∪ B (A union B) is all elements that are either in A OR B, or both.
A ∩ B (A intersect B) is all elements that are in both A AND B.
If A ∩ B = {}, then A and B are disjoint.
|A ∪ B| = |A| + |B| - |A ∩ B| (principle of inclusion-exclusion)
A - B (reads "set A without set B") is all elements in A not in B.
The universal set is the set that contains all elements, including itself.
_
Given U=universal set, A (the complement of A) is the set U - A.
See /Material/ch01/set_identities
A bit string can be used to represent a subset of U, where U is an ordered
set. A '1' denotes the member in that position in U is in the subset, and
'0' denotes the member in that position in U is not in the subset. Given
U::={2,4,6,8,10,12} A::={4,8,12} B::={2,4,6}
A's bit string is 010101 and B's bit string is = 111000.
The union and intersection operations are bitwise OR and AND respectively:
A ∪ B is 010101 OR 111000 = 111101 which is {2,4,6,8,12}
A ∩ B is 010101 AND 111000 = 010000 which is {4}
Problems:
Find the sets A and B if A-B={1,5,7,8}, B-A={2,10}, and A ∩ B={3,6,9}
From A-B = {1,5,7,8} we know that 1,5,7,8 are elements in A and not B
From B-A = {2,10}, we know that 2,10 are elements of B and not A
From A ∩ B = {3,6,9} we know that 3,6,9 and elements in both A and B
Thus, A={1,3,5,6,7,9} and B={2,3,6,9,10}.
Venn diagrams are used to represent the relationships between and among
sets. Two sets and the universal set U result in 4 distinct areas:
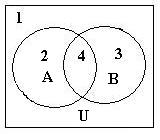 U is 1,2,3,4.
A ∪ B is 2,3,4.
A ∩ B is 4.
A - B is 2.
B - A is 3.
_
A is 1,3.
_____
A ∪ B is 1.
_ _
A ∩ B is 1.
_ _
A ∪ B is 1,2,3.
_____
A ∩ B is 1,2,3.
(A - B) ∪ (B - A) is 2,3.
((A ∪ B) - (A ∩ B)) is 2,3.
__________________
(A - B) ∪ (B - A) is 1,4.
(U - (A ∪ B)) ∪ (A - B) is 1,2.
_
B is 1,2.
Set membership tables are used to show set equality. If the final
result columns are equal, then the sets are equal.
Example 1.
_
(U - (A u B)) u (A - B) = B
_
A B (U - (A u B)) u (A - B) B
--- ---------------------- ---
1 1 1 0 1 |0| 0 |0|
1 0 1 0 1 |1| 1 |1|
0 1 1 0 1 |0| 0 |0|
0 0 1 1 0 |1| 0 |1|
Example 2.
___________ _ _ _
A u (B n C) = (C u B) n A.
___________ _ _ _
A B C A u (B n C) A u (B n C) (C u B) n A
----- ------------ ----------- --------------
1 1 1 1 1 |0| 0 0 0 |0| 0
1 1 0 1 0 |0| 1 1 0 |0| 0
1 0 1 1 0 |0| 0 1 1 |0| 0
1 0 0 1 0 |0| 1 1 1 |0| 0
0 1 1 1 1 |0| 0 0 0 |0| 1
0 1 0 0 0 |1| 1 1 0 |1| 1
0 0 1 0 0 |1| 0 1 1 |1| 1
0 0 0 0 0 |1| 1 1 1 |1| 1
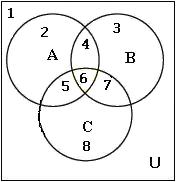
Three sets A, B, C, and U result in 8 areas of interaction:
U is 1,2,3,4.
A ∪ B is 2,3,4.
A ∩ B is 4.
A - B is 2.
B - A is 3.
_
A is 1,3.
_____
A ∪ B is 1.
_ _
A ∩ B is 1.
_ _
A ∪ B is 1,2,3.
_____
A ∩ B is 1,2,3.
(A - B) ∪ (B - A) is 2,3.
((A ∪ B) - (A ∩ B)) is 2,3.
__________________
(A - B) ∪ (B - A) is 1,4.
(U - (A ∪ B)) ∪ (A - B) is 1,2.
_
B is 1,2.
Set membership tables are used to show set equality. If the final
result columns are equal, then the sets are equal.
Example 1.
_
(U - (A u B)) u (A - B) = B
_
A B (U - (A u B)) u (A - B) B
--- ---------------------- ---
1 1 1 0 1 |0| 0 |0|
1 0 1 0 1 |1| 1 |1|
0 1 1 0 1 |0| 0 |0|
0 0 1 1 0 |1| 0 |1|
Example 2.
___________ _ _ _
A u (B n C) = (C u B) n A.
___________ _ _ _
A B C A u (B n C) A u (B n C) (C u B) n A
----- ------------ ----------- --------------
1 1 1 1 1 |0| 0 0 0 |0| 0
1 1 0 1 0 |0| 1 1 0 |0| 0
1 0 1 1 0 |0| 0 1 1 |0| 0
1 0 0 1 0 |0| 1 1 1 |0| 0
0 1 1 1 1 |0| 0 0 0 |0| 1
0 1 0 0 0 |1| 1 1 0 |1| 1
0 0 1 0 0 |1| 0 1 1 |1| 1
0 0 0 0 0 |1| 1 1 1 |1| 1
Three sets A, B, C, and U result in 8 areas of interaction:
 Set identities can also show equivalence.
Set Identities
A,B are sets; U=Universal Set; u is union; n is intersection; ' is complement
-------------------------------------------------------------------------------
A u {} = A Identity Laws
A n U = A
-------------------------------------------------------------------------------
A u U = U Domination Laws
A n {} = {}
-------------------------------------------------------------------------------
A u A = A Idempotent Laws
A n A = A
-------------------------------------------------------------------------------
A'' = A Complementation Law
-------------------------------------------------------------------------------
A u B = B u A Commutative Laws
A n B = B n A
-------------------------------------------------------------------------------
(A u B) u C = A u (B u C) Associativity Laws
A n (B n C) = (A n B) n C
-------------------------------------------------------------------------------
A u (B n C) = (A u B) n (A u C) Distributive Laws
A n (B u C) = (A n B) u (A n C)
-------------------------------------------------------------------------------
(A u B)' = A' n B' De Morgan's Laws
(A n B)' = A' u B'
-------------------------------------------------------------------------------
A u A' = U Complement Laws
A n A' = {}
-------------------------------------------------------------------------------
___________ _ _ _
A u (B n C) = (C u B) n A.
___________ _ _______
A u (B n C) = A n (B n C) De Morgan's
_ _ _
= A n (B u C) De Morgan's
_ _ _
= A n (C u B) Commutativity
_ _ _
= (C u B) n A Commutativity
Set identities can also show equivalence.
Set Identities
A,B are sets; U=Universal Set; u is union; n is intersection; ' is complement
-------------------------------------------------------------------------------
A u {} = A Identity Laws
A n U = A
-------------------------------------------------------------------------------
A u U = U Domination Laws
A n {} = {}
-------------------------------------------------------------------------------
A u A = A Idempotent Laws
A n A = A
-------------------------------------------------------------------------------
A'' = A Complementation Law
-------------------------------------------------------------------------------
A u B = B u A Commutative Laws
A n B = B n A
-------------------------------------------------------------------------------
(A u B) u C = A u (B u C) Associativity Laws
A n (B n C) = (A n B) n C
-------------------------------------------------------------------------------
A u (B n C) = (A u B) n (A u C) Distributive Laws
A n (B u C) = (A n B) u (A n C)
-------------------------------------------------------------------------------
(A u B)' = A' n B' De Morgan's Laws
(A n B)' = A' u B'
-------------------------------------------------------------------------------
A u A' = U Complement Laws
A n A' = {}
-------------------------------------------------------------------------------
___________ _ _ _
A u (B n C) = (C u B) n A.
___________ _ _______
A u (B n C) = A n (B n C) De Morgan's
_ _ _
= A n (B u C) De Morgan's
_ _ _
= A n (C u B) Commutativity
_ _ _
= (C u B) n A Commutativity
 U is 1,2,3,4.
A ∪ B is 2,3,4.
A ∩ B is 4.
A - B is 2.
B - A is 3.
_
A is 1,3.
_____
A ∪ B is 1.
_ _
A ∩ B is 1.
_ _
A ∪ B is 1,2,3.
_____
A ∩ B is 1,2,3.
(A - B) ∪ (B - A) is 2,3.
((A ∪ B) - (A ∩ B)) is 2,3.
__________________
(A - B) ∪ (B - A) is 1,4.
(U - (A ∪ B)) ∪ (A - B) is 1,2.
_
B is 1,2.
Set membership tables are used to show set equality. If the final
result columns are equal, then the sets are equal.
Example 1.
_
(U - (A u B)) u (A - B) = B
_
A B (U - (A u B)) u (A - B) B
--- ---------------------- ---
1 1 1 0 1 |0| 0 |0|
1 0 1 0 1 |1| 1 |1|
0 1 1 0 1 |0| 0 |0|
0 0 1 1 0 |1| 0 |1|
Example 2.
___________ _ _ _
A u (B n C) = (C u B) n A.
___________ _ _ _
A B C A u (B n C) A u (B n C) (C u B) n A
----- ------------ ----------- --------------
1 1 1 1 1 |0| 0 0 0 |0| 0
1 1 0 1 0 |0| 1 1 0 |0| 0
1 0 1 1 0 |0| 0 1 1 |0| 0
1 0 0 1 0 |0| 1 1 1 |0| 0
0 1 1 1 1 |0| 0 0 0 |0| 1
0 1 0 0 0 |1| 1 1 0 |1| 1
0 0 1 0 0 |1| 0 1 1 |1| 1
0 0 0 0 0 |1| 1 1 1 |1| 1
Three sets A, B, C, and U result in 8 areas of interaction:
U is 1,2,3,4.
A ∪ B is 2,3,4.
A ∩ B is 4.
A - B is 2.
B - A is 3.
_
A is 1,3.
_____
A ∪ B is 1.
_ _
A ∩ B is 1.
_ _
A ∪ B is 1,2,3.
_____
A ∩ B is 1,2,3.
(A - B) ∪ (B - A) is 2,3.
((A ∪ B) - (A ∩ B)) is 2,3.
__________________
(A - B) ∪ (B - A) is 1,4.
(U - (A ∪ B)) ∪ (A - B) is 1,2.
_
B is 1,2.
Set membership tables are used to show set equality. If the final
result columns are equal, then the sets are equal.
Example 1.
_
(U - (A u B)) u (A - B) = B
_
A B (U - (A u B)) u (A - B) B
--- ---------------------- ---
1 1 1 0 1 |0| 0 |0|
1 0 1 0 1 |1| 1 |1|
0 1 1 0 1 |0| 0 |0|
0 0 1 1 0 |1| 0 |1|
Example 2.
___________ _ _ _
A u (B n C) = (C u B) n A.
___________ _ _ _
A B C A u (B n C) A u (B n C) (C u B) n A
----- ------------ ----------- --------------
1 1 1 1 1 |0| 0 0 0 |0| 0
1 1 0 1 0 |0| 1 1 0 |0| 0
1 0 1 1 0 |0| 0 1 1 |0| 0
1 0 0 1 0 |0| 1 1 1 |0| 0
0 1 1 1 1 |0| 0 0 0 |0| 1
0 1 0 0 0 |1| 1 1 0 |1| 1
0 0 1 0 0 |1| 0 1 1 |1| 1
0 0 0 0 0 |1| 1 1 1 |1| 1
Three sets A, B, C, and U result in 8 areas of interaction:
 Set identities can also show equivalence.
Set Identities
A,B are sets; U=Universal Set; u is union; n is intersection; ' is complement
-------------------------------------------------------------------------------
A u {} = A Identity Laws
A n U = A
-------------------------------------------------------------------------------
A u U = U Domination Laws
A n {} = {}
-------------------------------------------------------------------------------
A u A = A Idempotent Laws
A n A = A
-------------------------------------------------------------------------------
A'' = A Complementation Law
-------------------------------------------------------------------------------
A u B = B u A Commutative Laws
A n B = B n A
-------------------------------------------------------------------------------
(A u B) u C = A u (B u C) Associativity Laws
A n (B n C) = (A n B) n C
-------------------------------------------------------------------------------
A u (B n C) = (A u B) n (A u C) Distributive Laws
A n (B u C) = (A n B) u (A n C)
-------------------------------------------------------------------------------
(A u B)' = A' n B' De Morgan's Laws
(A n B)' = A' u B'
-------------------------------------------------------------------------------
A u A' = U Complement Laws
A n A' = {}
-------------------------------------------------------------------------------
___________ _ _ _
A u (B n C) = (C u B) n A.
___________ _ _______
A u (B n C) = A n (B n C) De Morgan's
_ _ _
= A n (B u C) De Morgan's
_ _ _
= A n (C u B) Commutativity
_ _ _
= (C u B) n A Commutativity
Set identities can also show equivalence.
Set Identities
A,B are sets; U=Universal Set; u is union; n is intersection; ' is complement
-------------------------------------------------------------------------------
A u {} = A Identity Laws
A n U = A
-------------------------------------------------------------------------------
A u U = U Domination Laws
A n {} = {}
-------------------------------------------------------------------------------
A u A = A Idempotent Laws
A n A = A
-------------------------------------------------------------------------------
A'' = A Complementation Law
-------------------------------------------------------------------------------
A u B = B u A Commutative Laws
A n B = B n A
-------------------------------------------------------------------------------
(A u B) u C = A u (B u C) Associativity Laws
A n (B n C) = (A n B) n C
-------------------------------------------------------------------------------
A u (B n C) = (A u B) n (A u C) Distributive Laws
A n (B u C) = (A n B) u (A n C)
-------------------------------------------------------------------------------
(A u B)' = A' n B' De Morgan's Laws
(A n B)' = A' u B'
-------------------------------------------------------------------------------
A u A' = U Complement Laws
A n A' = {}
-------------------------------------------------------------------------------
___________ _ _ _
A u (B n C) = (C u B) n A.
___________ _ _______
A u (B n C) = A n (B n C) De Morgan's
_ _ _
= A n (B u C) De Morgan's
_ _ _
= A n (C u B) Commutativity
_ _ _
= (C u B) n A Commutativity