See graph sketcher
==============================================================================
Notation:
Z = { .... -2, -1, 0, 1, 2, .... }, the set of integers
Z+ = {1, 2, .... }, the set of positive integers
N = { 0, 1, 2, .... }, the set of natural numbers
Q = { p/q | p isin Z, q isin Z, q != 0} , the set of rational numbers
R is the set of real numbers
============================================================================
A function is a relation from a set of inputs A to a set of possible outputs B
where each input is related to exactly one output. If not all inputs in A
are mapped, this is a not a function but a *partial function.* If an element
in A maps to multiple elements in B, this is not a function.
The signature of a function is its mapping from domain to codomain:
f: R -> R
A function f: A -> B is discrete if A and B are finite or countable.
A domain is countable if it can be indexed by Z.
The range of a function f is the set of all f(a), 'a' ∈ the domain and
f(a) ∈ the codomain.
==============================================================================
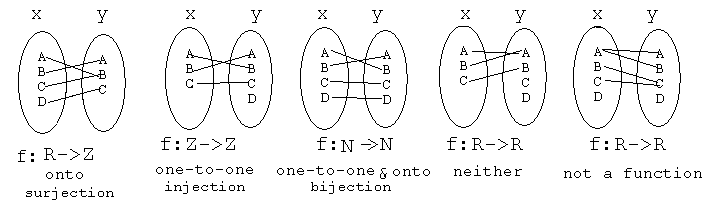
Function mappings are identified by the following properties:
One-to-One (Injective Functions) - every element in the domain is mapped to
at most one element in the codomain
Onto (Surjective Functions) - every element in the codomain has at least one
mapping
One-to-One and Onto (Bijective Functions) - every element in the codomain has
one and only one mapping
 ==============================================================================
The identity function on A is defined as
f: A -> A
f(x) = x
The identity function is one-to-one and onto.
==============================================================================
Inverse Functions.
********************************************************************
* function f will have an inverse if and only if f is a bijection *
********************************************************************
Assume f: A -> B is one-to-one and onto.
The inverse f^-1: B -> A, is a function that maps every b in B to a unique a
in A, such that f(a) = b.
If function g is the inverse of function f, then f(x) = y and g(y) = x.
Let f(x) = lg x. (lg is log_2)
Let g(x) = 2^x.
Then f and g are inverse functions; e.g., f(1024) = 10. g(10) = 1024.
------------------------
| Function Composition |
------------------------
f o g = f(g(x)) (reads "f of g of x" or "f compose g")
To compute you apply g to x then apply f to g(x). The output
of g becomes the input of f.
If f and g are inverses then f(g(x) = x. Example:
Let g(x) = 2^x. Let f(x) = lg x. Then f(g(x)) = x.
For x=10. Apply g: 2^x = 1024. Apply f: lg(1024) = 10.
lg(2^10) = 10.
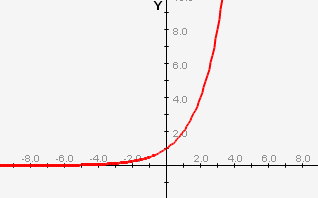
The graph below is g(x) = 2^x.
==============================================================================
The identity function on A is defined as
f: A -> A
f(x) = x
The identity function is one-to-one and onto.
==============================================================================
Inverse Functions.
********************************************************************
* function f will have an inverse if and only if f is a bijection *
********************************************************************
Assume f: A -> B is one-to-one and onto.
The inverse f^-1: B -> A, is a function that maps every b in B to a unique a
in A, such that f(a) = b.
If function g is the inverse of function f, then f(x) = y and g(y) = x.
Let f(x) = lg x. (lg is log_2)
Let g(x) = 2^x.
Then f and g are inverse functions; e.g., f(1024) = 10. g(10) = 1024.
------------------------
| Function Composition |
------------------------
f o g = f(g(x)) (reads "f of g of x" or "f compose g")
To compute you apply g to x then apply f to g(x). The output
of g becomes the input of f.
If f and g are inverses then f(g(x) = x. Example:
Let g(x) = 2^x. Let f(x) = lg x. Then f(g(x)) = x.
For x=10. Apply g: 2^x = 1024. Apply f: lg(1024) = 10.
lg(2^10) = 10.
The graph below is g(x) = 2^x.
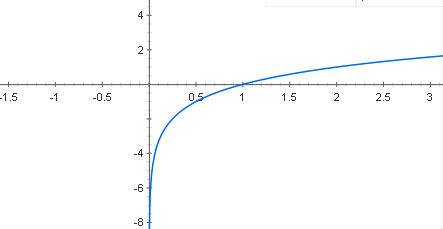
 The graph below is f(x) = lg x.
The graph below is f(x) = lg x.
 Function composition is not commutative.
f o g is not the same as g o f (although there are some exceptions).
More function composition.
Ex.
f: R -> Z
f(x) = ceil(x) + 1
g: Z -> R
g(x) = 3.5x
f o g: Z -> R -> Z
f o g = f(g(x))
= ceil(3.5x) + 1
g o f : R -> Z -> R
g o f = g(f(x))
= 3.5(ceil(x) + 1)
= 3.5(ceil(x)) + 3.5
Another example:
f: Z -> Q (Q is set of rational numbers)
f(x) = x/3
solve for x to find the inverse, i.e. f^-1:
y = x/3
x = 3y
call the inverse g
g: Q -> Z
g(x) = 3x
Q -> Z -> Q <= identity on Q
f o g = f(g(x))
= (3x)/3
= x
Z -> Q -> Z <= identity on Z
g o f = g(f(x))
= 3 (x/3)
= x
The composition of a function and its inverse is an identity function, in
either direction; e.g., f(g(x)) = x and g(f(x)) = x.
Let g(x)=2^x. Let f(x)=lg x. Then f(g(x)) is lg(2^x) and g(f(x))=2^(lg x).
lg(2^5) = 5. and 2^(lg 32) = 32
==============================================================================
floor and ceiling functions are frequently used in computer science.
the mapping of floor and ceiling is always from the set of real numbers to
the set of integers.
Useful properties of floor and ceiling functions, where n is an integer and
x is a real number or an integer.
ceil(x) is the smallest integer not smaller than x.
ceil(5.3) = 6 ceil(5) = 5
floor(x) is the largest integer not larger than x.
floor(5.3) = 5 floor(5) = 5
From these definitions,
floor(x) = n iff n <= x < n + 1
ceil(x) = n iff n - 1 < x <= n
floor(x) = n iff x - 1 < n <= x
ceil(x) = n iff x <= n < x + 1
floor(x+n) = floor(x) + n
ceil(x + n) = ceil(x) + n
ceil(n) = floor(m), where n and m are integers and n=m.
==============================================================================
functions in a programming language
/* g: Z -> R, g(x) = 2x/3 */
double g ( int x) {
return (2*x)/3;
}
/* f o g: Z -> R -> Z, f(x) = ceil(x) + 2, g(x) = 2x/3 */
int f ( int x) {
return ceil(g(x)) + 2;
}
What is the composition f o g?
f(g(x)) is ceil(2x/3) + 2
What is the signature of f o g?
f: Z -> R -> Z
==============================================================================
// another example
int mod4 ( int x )
{
return x % 4;
}
ANSI-C:
The % operator divides the first operand x by the second y and yields the
remainder. Both operands must be integral. When both operands are unsigned or
positive, the result is positive. If either operand is negative, the sign of
the result is the same as the sign of the left operand. If x < y, then
x mod y = x.
Q: What is the signature of the mod4 function above?
Z -> { -3, -2, -1, 0, 1, 2, 3 }
Q: Is mod4 one-to-one?
no. mod4(13) = 1 and mod4(1) = 1
onto?
yes. every value in the codomain is mapped.
a bijection?
no. since it is not one-to-one, it is not a bijection and does not have an
inverse.
==============================================================================
The Hamming Distance between two bit strings B1 and B2 is the number of bits
that differ between B1 and B2; i.e. the sum of 1s in (B1 XOR B2).
Ex.
10101010 10100000 10100000 11100000
01010101 10100000 10100111 00000000
-------- -------- -------- ---------
11111111 = 8 00000000 = 0 00000111 = 3 11100000 = 3
Q: What is the signature of this function?
f: {2-byte bit strings x 2-byte bit strings} -> {0...8}
Q: Is this function one-to-one?
no.
onto?
yes.
a bijection? no. does it have an inverse? no.
==============================================================================
A cipher is a mapping from readable words in English (plaintext) to words that
are not readable (ciphertext). A substitution cipher applies a key to the
plaintext to create a permutation.
Assume words are written in the 26 lower case letters of the alphabet with no
spaces between words. A simple substitution cipher permutes the plaintext by
shifting every letter 3 letters to the right:
plaintext: abcdefghijklmnopqrstuvwxyz
ciphertext: xyzabcdefghijklmnopqrstuvw
plaintext: hellothere
ciphertext: ebiilqebob
Q: What is the signature of the function that encodes a single letter x, such
that x + n returns the letter shifted n to the right?
f: {a-z} -> {a-z}
Q: Is this function one-to-one? yes. onto? yes. is there an inverse? yes.
if so, what is it? the inverse is applying the cipher in reverse (i.e. shift
all letters in the ciphertext 3 letters to the LEFT to get the key).
Conclusion:
A permutation is a bijection in which the domain and the codomain are the
same. In general, you want cipher functions to be bijections.
==============================================================================
Ciphers can be used for something other than secrecy. On solaris a checksum
computes a 128-bit number from a file using the MD5 message digest algorithm.
Checksums are used as fingerprints to identify a file; i.e. can determine the
authenticity of the file.
Assume a checksum algorithm that simply sums the number of 1s in the binary
encoding of the file. Assume the file also contains numbers. For simplicity,
assume a checksum function that is applied to 4 bytes of the file at a time.
Q: What is the signature of the checksum function?
f: { all 4-byte bit strings } -> {0,1,2...32}
Q: Is this function one-to-one? no. onto? yes. is there an inverse? no.
Since a checksum does not need to be reversed the checksum function does not
need to be a bijection.
Assume the only strings you are applying a checksum to are those that encode
valid English words and the encoding is extended-ASCII (8 bytes). How do the
domain and codomain differ from the above function?
The domain consists of only those 4-byte bit strings that correspond to valid
word segments in English. For example, 'xxxx'is not in the domain. In this
case, if the codomain is {0-32}, the function is not onto.
Function composition is not commutative.
f o g is not the same as g o f (although there are some exceptions).
More function composition.
Ex.
f: R -> Z
f(x) = ceil(x) + 1
g: Z -> R
g(x) = 3.5x
f o g: Z -> R -> Z
f o g = f(g(x))
= ceil(3.5x) + 1
g o f : R -> Z -> R
g o f = g(f(x))
= 3.5(ceil(x) + 1)
= 3.5(ceil(x)) + 3.5
Another example:
f: Z -> Q (Q is set of rational numbers)
f(x) = x/3
solve for x to find the inverse, i.e. f^-1:
y = x/3
x = 3y
call the inverse g
g: Q -> Z
g(x) = 3x
Q -> Z -> Q <= identity on Q
f o g = f(g(x))
= (3x)/3
= x
Z -> Q -> Z <= identity on Z
g o f = g(f(x))
= 3 (x/3)
= x
The composition of a function and its inverse is an identity function, in
either direction; e.g., f(g(x)) = x and g(f(x)) = x.
Let g(x)=2^x. Let f(x)=lg x. Then f(g(x)) is lg(2^x) and g(f(x))=2^(lg x).
lg(2^5) = 5. and 2^(lg 32) = 32
==============================================================================
floor and ceiling functions are frequently used in computer science.
the mapping of floor and ceiling is always from the set of real numbers to
the set of integers.
Useful properties of floor and ceiling functions, where n is an integer and
x is a real number or an integer.
ceil(x) is the smallest integer not smaller than x.
ceil(5.3) = 6 ceil(5) = 5
floor(x) is the largest integer not larger than x.
floor(5.3) = 5 floor(5) = 5
From these definitions,
floor(x) = n iff n <= x < n + 1
ceil(x) = n iff n - 1 < x <= n
floor(x) = n iff x - 1 < n <= x
ceil(x) = n iff x <= n < x + 1
floor(x+n) = floor(x) + n
ceil(x + n) = ceil(x) + n
ceil(n) = floor(m), where n and m are integers and n=m.
==============================================================================
functions in a programming language
/* g: Z -> R, g(x) = 2x/3 */
double g ( int x) {
return (2*x)/3;
}
/* f o g: Z -> R -> Z, f(x) = ceil(x) + 2, g(x) = 2x/3 */
int f ( int x) {
return ceil(g(x)) + 2;
}
What is the composition f o g?
f(g(x)) is ceil(2x/3) + 2
What is the signature of f o g?
f: Z -> R -> Z
==============================================================================
// another example
int mod4 ( int x )
{
return x % 4;
}
ANSI-C:
The % operator divides the first operand x by the second y and yields the
remainder. Both operands must be integral. When both operands are unsigned or
positive, the result is positive. If either operand is negative, the sign of
the result is the same as the sign of the left operand. If x < y, then
x mod y = x.
Q: What is the signature of the mod4 function above?
Z -> { -3, -2, -1, 0, 1, 2, 3 }
Q: Is mod4 one-to-one?
no. mod4(13) = 1 and mod4(1) = 1
onto?
yes. every value in the codomain is mapped.
a bijection?
no. since it is not one-to-one, it is not a bijection and does not have an
inverse.
==============================================================================
The Hamming Distance between two bit strings B1 and B2 is the number of bits
that differ between B1 and B2; i.e. the sum of 1s in (B1 XOR B2).
Ex.
10101010 10100000 10100000 11100000
01010101 10100000 10100111 00000000
-------- -------- -------- ---------
11111111 = 8 00000000 = 0 00000111 = 3 11100000 = 3
Q: What is the signature of this function?
f: {2-byte bit strings x 2-byte bit strings} -> {0...8}
Q: Is this function one-to-one?
no.
onto?
yes.
a bijection? no. does it have an inverse? no.
==============================================================================
A cipher is a mapping from readable words in English (plaintext) to words that
are not readable (ciphertext). A substitution cipher applies a key to the
plaintext to create a permutation.
Assume words are written in the 26 lower case letters of the alphabet with no
spaces between words. A simple substitution cipher permutes the plaintext by
shifting every letter 3 letters to the right:
plaintext: abcdefghijklmnopqrstuvwxyz
ciphertext: xyzabcdefghijklmnopqrstuvw
plaintext: hellothere
ciphertext: ebiilqebob
Q: What is the signature of the function that encodes a single letter x, such
that x + n returns the letter shifted n to the right?
f: {a-z} -> {a-z}
Q: Is this function one-to-one? yes. onto? yes. is there an inverse? yes.
if so, what is it? the inverse is applying the cipher in reverse (i.e. shift
all letters in the ciphertext 3 letters to the LEFT to get the key).
Conclusion:
A permutation is a bijection in which the domain and the codomain are the
same. In general, you want cipher functions to be bijections.
==============================================================================
Ciphers can be used for something other than secrecy. On solaris a checksum
computes a 128-bit number from a file using the MD5 message digest algorithm.
Checksums are used as fingerprints to identify a file; i.e. can determine the
authenticity of the file.
Assume a checksum algorithm that simply sums the number of 1s in the binary
encoding of the file. Assume the file also contains numbers. For simplicity,
assume a checksum function that is applied to 4 bytes of the file at a time.
Q: What is the signature of the checksum function?
f: { all 4-byte bit strings } -> {0,1,2...32}
Q: Is this function one-to-one? no. onto? yes. is there an inverse? no.
Since a checksum does not need to be reversed the checksum function does not
need to be a bijection.
Assume the only strings you are applying a checksum to are those that encode
valid English words and the encoding is extended-ASCII (8 bytes). How do the
domain and codomain differ from the above function?
The domain consists of only those 4-byte bit strings that correspond to valid
word segments in English. For example, 'xxxx'is not in the domain. In this
case, if the codomain is {0-32}, the function is not onto.