Discrete p(E) = the probability of a certain countable event occurring. For example, the sides of a die can be counted (there are 6). 1/6 is the probability of a particular side occurring when you roll the die. The sample set is discrete and countable. The probability that a range of temperatures may occur on a certain day, for example, is non-discrete.
Finite probability defines the chances of a countable event occurring out of a finite number of outcomes. Let S, the Sample Space, be a finite set containing all equally likely outcomes. Let E, the Event Space, be a subset of S that contains the successful outcomes.
The probability of event E occurring out of all possible outcomes in S is a ratio: the cardinality of E over the cardinality of S. Since both S and E are finite sets, and E is a subset of S, probability p is a rational number <= 1 and >= 0.
Laplace's Definition 1.
|E|
p(E) = --- // the probability of event E occurring
|S|
___ |S| - |E|
p(E) = --------- // the probability of event E not occurring
|S|
Observations:
p(E) is a ratio from 0 to 1: 0 <= p(E) <= 1.
p(E) = 0 means E has zero probability of occurring.
p(E) = 1 means E has 100% probability of occurring.
1 - p(E) is the probability of E *not* occurring.
Finite probability is a counting problem. To find p(E),
Step 1. Determine |S|, which is the number of all possible outcomes.
Step 2. Determine |E|, which is how many times the event occurs in S.
Step 3. Compute the ratio |E|/|S|.
In the notes below I do not reduce |E|/|S| in order to clearly see the ratio.
EXAMPLES:
Q: What is the probability of winning the lottery by selecting the correct six
integers between 1 and 52, where order does not matter.
|S| = C(52,6)
|E| = C(1,1) // there is only one winning ticket
p(E) = 1/C(52,6) = 1/20,358,520
The next questions concern rolling a single die. A die has 6 sides, labeled
1..6. When you roll a die, assuming any outcome is equally likely, |S| is 6.
Q: What is the probability that a die comes up six when it is rolled?
There is only one way this can occur, thus
p(E) = 1/6.
Q: What is the probability that a die comes up six OR four when it is rolled?
This counting problem uses the Sum Rule. There is one way to get a 6. There
is one way to get a four. Both outcomes are in E, thus |E| = 1+1.
p(E) = 2/6.
Now consider the probability of a certain outcome occurring when two dice
are rolled. S in this case contains all 2-tuples of the form (x,y), where x
is the value of one die and y is the value of the other. There are thus 6*6
possible outcomes in S. |S| = 36.
Q: What is the probability that the sum of the dice is 7? (i.e., x + y = 7)
E = {(1,6), (6,1), (2,5), (5,2), (3,4), (4,3) }. |E| = 6.
p(E) = 6/36.
Q: What is the probability that you get (6 AND 4) when the dice are rolled?
There are only two successful outcomes in E: (6,4) and (4,6). Thus
p(E) = 2/36.
Q: What is the probability that you get (6 OR 4) when the dice are rolled?
Let's do a brute force approach. There are 36 possible 2-tuple outcomes in S,
shown below with the number of successful outcomes in each row summed:
S = { (1,1), (1,2), (1,3), (1,4), (1,5), (1,6), 2
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6), 2
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6), 2
(4,1), (4,2), (4,3), (4,4), (4,5), (4,6), 6
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6), 2
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)} 6
===
|E| = 20
p(E) = 20/36.
When you count |E|, you are applying the inclusion-exclusion rule:
There are 2 * 6 = 12 ways to get a 4 or 6 in the first die and anything in
the second die.
There are 2 * 6 = 12 ways to get a 4 or 6 in the second die and anything in
the first die.
There are 4 duplicates (4,4), (4,6) and (6,4), (6,6) that you must exclude.
12+12-4=20.
In general, when asked to find the probability that E1 OR E2 will occur you
are interested in |E1 U E2|.
By the inclusion-exclusion rule, |E1 U E2| = |E1| + |E2| - |E1 n E2|.
The probability that E1 or E2 will occur is thus:
|E1| + |E2| - |E1 n E2|
p(E1 | E2) = -----------------------
|S|
Given two events E1 and E2 in the same sample space S, the probability that
E1 and E2 both occur is the probability of the intersection of E1 and E2:
|E1 n E2|
p(E1 ^ E2) = ----------
|S|
If you know p(E1), p(E2) and p(E1 ^ E2) you can directly apply this rule:
Rule 1. p(E1 | E2) = p(E1) + p(E1) - p(E1 ^ E2).
For example, what is the probability that you will roll two die and get a 4 or
a 6? We concluded above that p(E1 U E2) = 20/36. By Rule 1:
p(E1 | E2) = (12/36 + 12/36) - (4/36)
= 24/36 - 4/36
= 20/36. bingo.
Q: What is the probability that a random sequence of 10 bits has exactly 7 1s?
Since S is all possible sequences of bits, |S| = 2^10.
E is all bit strings that contain exactly 7 bits of value 1. This is a
counting problem where you pick the 7 positions that you want 1s in: C(10,7).
p(E) = C(10,7)/2^10.
C(10,4) = 10*9*8/3*2
= 5*3*8
= 120.
p(E) = 120/2^10, which is roughly 12%.
This number, btw, is the same for the number of random sequences of 10 bits
= with 3 0s.
= with 3 1s.
= with 7 0s.
Q: What is the probability that a random sequence of 10 bits has at least one 0?
Hint: Since this means 1 zero or 2 zeros or 3 zeros, etc. To count this,
it is easier to compute the complement, which is the number of strings
without a zero. There is one string with no zeros, thus
|E| = 2^10 - 1.
|S| = 2^10, the number of all possible bit strings of length 10.
2^10 - 1
p(E) = ---------
2^10
= 1023/1024.
Q: What is probability that a positive integer selected at random from the set
S of positive integers <= 100, |S| = 100, is
divisible by 2? (call this event E1)
|E1|: floor(100/2) = 50; p(E1) = 50/100 = 1/2
divisible by 5? (call this event E2)
|E2|: floor(100/5) = 20; p(E2) = 20/100 = 1/5
divisible by 2 and 5? (call this event E3)
|E3|: floor(100/10) = 10; p(E1 n E2) = 10/100 = 1/10
divisible by 2 or 5? (call this event E4)
p(E4) = p(E1) + p(E2) - p(E1 n E2) = 1/2 + 1/5 - 1/10 = 3/5
/// Note: a few of the concepts below are from Section 6.2
If there is a finite number n of equally likely outcomes, the probability of
the event E is the sum of the probabilities of the outcomes in E.
p(E) is the summation of p(s) for all s in E.
This agrees with Definition 1 above.
Example. You have a bag of 10 marbles, all different colors. What is the
probability that you will randomly pick the orange marble, if all picks are
equally likely? 1/10. The yellow marble? 1/10. The green marble? 1/10. The
yellow and green? 1/10 + /10 = 2/10. The probability that you will pick any
one of 5 out of 10 colors is:
p(E) = 1/10 + 1/10 + 1/10 + 1/10 + 1/10
= 1/2.
m
To generalize: p(E) = [ 1/n = m/n.
i=1
The bag contains 9 red marbles, 7 white marbles, and 5 blue marbles for a
total of 21. You grab 4 of the marbles. What is the probability that:
Q: What is the probability that you grab 2 white and 2 blue?
All possible outcomes is C(21,4). Now count events. There are C(7,2) ways to
grab 2 white marbles and C(5,2) ways to grab 2 blue marbles. Since you must
grab 2 white and 2 blue you apply the product rule. The final answer is:
C(7,2)C(5,2) (21)(10)
p(E) = ------------ = -------- = .035
C(21,4) 5985
Q: What is the probability that the marbles are not all the same color?
The easiest way to answer this is to find the probability that the marbles ARE
the same color and subtract this probability from 1. We do that first.
All possible outcomes is C(21,4). Now count events. There are C(9,4) ways to
grab all red marbles. There are C(7,4) ways to grab all white marbles. There
are C(5,4) ways to grab all blue marbles. Since the problem is all red OR
all white OR all blue you apply the inclusion/exclusion rule. Thus:
C(9,4) + C(7,4) + C(5,4) 126 + 35 + 5 166
p(E) = ----------------------- = ------------ = ---- = .028
C(21,4) 5985 5985
We can now determine the probability that are marbles are NOT the same color:
p(E) = 1 - .028
= .972
///
Suppose the outcomes are biased. For example, assume you are twice as likely
to pick red or blue than another color. In this case, your summation will look
like this, assuming your event is that you will pick one marble (probability
of 1):
p(E) = 2/12 + 2/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12
red blue
/// Independent Events
If the probability that two events E1 and E2 occur is
p(E1 and E2) = p(E1) * p(E2)
then E1 and E2 are independent events. This means that whether E1 occurs or
not is not influenced by knowing whether E2 occurs or not.
Q1: What is the probability that if a die is rolled two times, you get a 1
followed by a 6?
Since these are independent events,
P(E) = 1/6 * 1/6 = 1/36
Note that the above question is not the same as Q2 below:
Q2: "What is the probability of getting a 1 and a 6 if you roll two dice?"
In Q2, the outcomes in S are 36 2-tuples. Two of those 2-tuples, (1,6) and
(6,1) are successful outcomes. In Q2, P(E) is 2/36.
In general, the probability that independent events E1, E2, ...En occur is
p(E1) * p(E2) * ... * p(En).
Q: What is the probability that if a coin is tossed six times in a row, it
lands heads every time?
p(E) = (1/2)^6 = 1/64
Confirmed by the earlier notation:
|E| 1
p(E) = --- = --
|S| 64 // where S is all 2^6 arrangements of 6 tosses
Q: What is the probability that if a coin is tossed six times in a row, you
get 2 heads on the first two tosses followed by anything else?
p(E) = (1/2)^2 * (1)^4 = 1/4
To confirm by the earlier notation: |S| is still all arrangements of six
tosses, but E is those arrangments beginning with HH, which is 2^4.
|E| 16 1
p(E) = --- = -- = --
|S| 64 4
Q: What is the probability that in 5 coin tosses, you get exactly 3 heads,
assuming still an equal probability for a head and for a tail?
p(E) = (ways you can get 3 heads in 5 tossed)*p(3 heads)*p(2 tails)
p(E) = C(5,3)* (1/2)^3 * (1/2)^2 = 10 * (1/2)^5 = .3125
Confirmed by:
|E| C(5,3) 10
p(E) = --- = ------ = -- = .3125
|S| 2^5 32
Q: What is the probability that in 5 coin tosses, you get exactly 3 heads,
assuming a biased probability of 2/3 for a head and 1/3 for a tail?
Since we want exactly 3 heads, we have to fix heads at 3 and tails at 2.
The probability for heads is (2/3)(2/3)(2/3). p(E) for tails is (1/3)(1/3).
In 5 tosses, there are C(5,3) ways to get exactly 3 heads. The final
p(E) = C(5,3)* (2/3)^3 * (1/3)^2 = 10 * 0.0329218107 = .329
Q: What is the probability that in 5 coin tosses, you get all heads,
assuming equal probability for a head and for a tail?
p(E) = C(5,5)* (1/2)^5 * (1/2)^0 = (1/2)^5 = .03125
Hmmm...a pattern appears to be evolving.
The behavior of experiments with only two possible outcomes (such as coin
tosses or bit flips) is called a Bernoulli trial.
THEOREM 1. Probability of k successes in n independent Bernoulli trials, where
probability of success p and failure q = 1 - p, is
C(n,k) p^k q^(n-k)
As a function of k, this is the binomial distribution. The sum of the
probabilities for k successes over 2^n independent trials, for
k = 0,1,2, ... n, is
n
(p + q)^n = [ C(n,k) p^k q^(n-k)
k=0
When the probability of success = probability of failure (i.e., 1/2) the
formula becomes:
n n
[ C(n,k) p^k q^(n-k) = .5^n [ C(n,k), since p = q = .5.
k=0 k=0
For example, assume 10 trials. Then
(p + q)^10 = C(10,0)p^0q^10 + C(10,1)p^1q^9 + C(10,2)p^2q^8 + C(10,3)p^3q^7 +
C(10,4)p^4q^6 + C(10,5)p^5q^5 + C(10,6)p^6q^4 + C(10,7)p^7q^3 +
C(10,8)p^8q^2 + C(10,9)p^9q^1 + C(10,10)p^10q^0.
Assume p = q = 1/2. Replace p and q with 1/2 and pull 1/2^10 out:
= 1/2^10( C(10,0) + C(10,1) + C(10,2) + C(10,3) + C(10,4) +
C(10,5) + C(10,6) + C(10,7) + C(10,8) + C(10,9) +
C(10,10)).
Replace C(n,k) in each term and solve:
= 1/2^10(1 + 10 + 45 + 120 + 210 + 252 + 210 + 120 + 45 + 10 + 1).
= 1/2^10 (1024)
= 1024/1024
= 1. bingo.
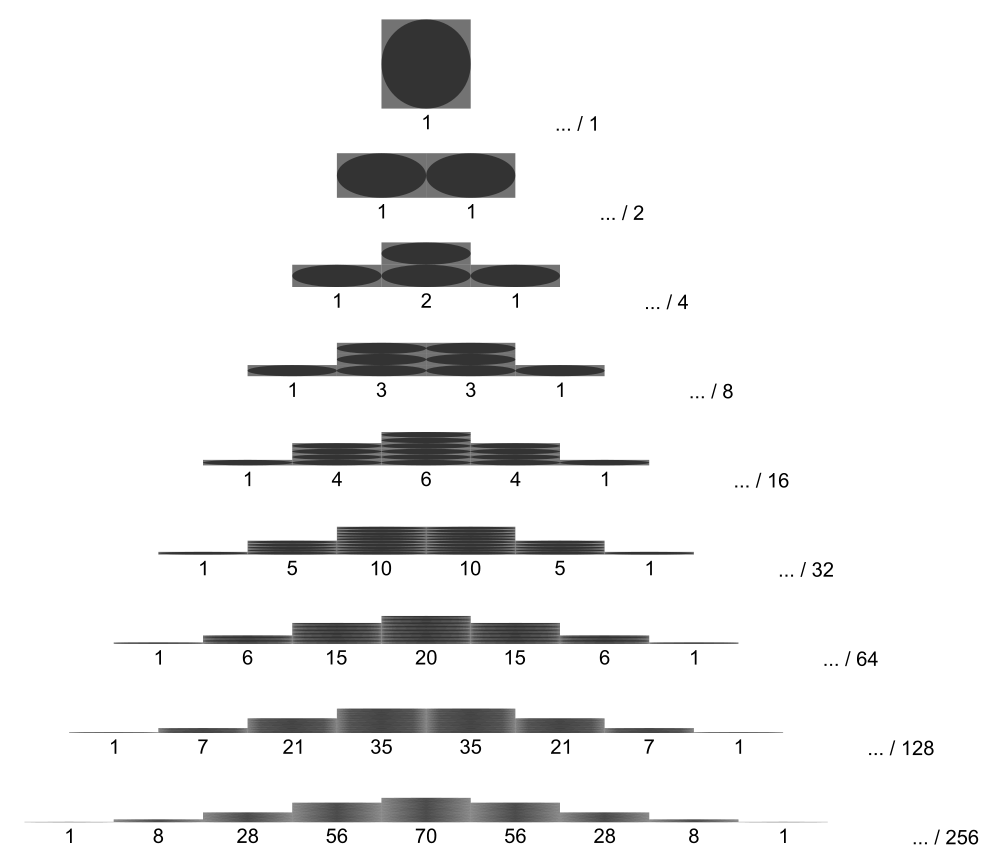
Since the nth row of Pascal's triangle represents all the ways you can
combine n things k at a time, k=0 to n, the sum of the coefficients is 2^n
and the denominator will always be 2^-n.
If you think of each *thing* as a trial with two possible results (success or
failure), then over 10 trials you have 2^10 possible outcomes. For example,
6 successes and 4 failures is one possibility. Each term represents the
probability of one outcome. The sum of all possible outcomes must be 1.
C(10,5) is the most likely outcome.
Plot the terms of (x + y)^10 for x=1 and y=1. (the graph is skewed on y-axis)
252 + *
| |
| |
| |
| |
210 + * | *
| | | |
| | | |
| | | |
120 + * | | | *
| | | | | |
| | | | | |
45 + * | | | | | *
C(n,k)x^(n-k)y^k | | | | | | | |
10 + * | | | | | | | *
| | | | | | | | | |
1 * | | | | | | | | | *
| | | | | | | | | | |
+--+--+--+--+--+--+--+--+--+--+--
k 0 1 2 3 4 5 6 7 8 9 10
Since x = y = 1, x^(n-k)y^k = C(n,k) for all terms. The summation of the points
(the terms in the expansion) is thus:
1 + 10 + 45 + 120 + 210 + 252 + 210 + 120 + 45 + 10 + 1 = 1024.
From the perspective of Pascal's Triangle, the behavior looks like this:

A hand is 5 cards. A deck is 52 cards. There are 4 suits and 13 types.
For poker S is the number of all possible 5-card hands out of 52 cards:
|S| = C(52,5)
= 2,598,960.
*Example*
What is the probability that a five-card poker hand contains 4-of-a-kind?
p(E) = C(13,1)C(4,4)C(48,1)/C(52,5)
*Example*
What is the probability that a five-card poker hand contains the ace of spades?
p(E) = C(1,1)C(51,4)/C(52,5) # pick ace of spades and pick other cards
= .096
*Example*
What is the probability that a five-card poker hand contains the two of
diamonds and the three of spades?
|E| = C(1,1)C(1,1)C(50,3)/C(52,5)
p(E) = .0075
*Example*
P(Full House) = C(13,1)C(4,2)C(12,1)C(4,3)/C(52,5)
pick face for pair. pick suit for pair. pick face for trips.pick suit for trips.
*Example*
What is the probability that a five-card poker hand contains exactly one king?
p(E) = C(4,1)C(48,4)/C(52,5) # exclude remaining kings from the other 4 cards
= 0.299
************************************
SUMMARY OF POKER HAND PROBABILITIES:
************************************
Unless otherwise stated, probabilities below are for *exactly* the type of
hand requested; i.e., the probability of one pair excludes 2 pair, 3-of-a-kind
and 4-of-a-kind. Exactly one pair* is:
C(13,1)C(4,2)C(12,3)C(4,1)C(4,1)C(4,1)
------------------------------------- = .4225
C(52,5)
Probability of poker hands
==========================
straight flush .0000015
4-of-a-kind .00024
full-house .00144
flush .00197
straight .00392
3-of-a-kind .0211
two pair .0475
one pair .4225
nothing .5011
==========
SUM 0.999999616
SINGLE PAIR
C(13,1)C(4,2)C(12,3)[(4,1)]^3/(52,5).
TWO PAIR
C(13,2)C(4,2)C(4,2)C(11,1)C(4,1)/C(52,5).
A TRIPLE (excludes 4 of a kind)
C(13,1)C(4,3)C(12,2)[4,1]^2/C(52,5).
A FULL HOUSE
C(13,1)C(4,3)C(12,1)C(4,2)/C(52,5).
FOUR OF A KIND
C(13,1)C(4,4)C(12,1)C(4,1)/C(52,5).
STRAIGHT
Five cards in a sequence (e.g., 4,5,6,7,8), with aces either low or high.
C(10,1)[4,1]^5/C(52,5).
FLUSH
5 cards from same suit
C(4,1)C(13,5)/C(52,5).
STRAIGHT FLUSH
5 cards of same suit and a straight
4*10/C(52,5).
ROYAL FLUSH
10,J,Q,K,A of one suit. 4/C(52,5).
NOTHING
(C(13,5)-10)(4^5-4)/C(52,5)
(subtract 10 straights and 4 patterns where all 5 cards have the same suit.)