Please do these steps to prepare for coding...

1. Log into Odin, using the -YC options.
   example: ssh myname@odin -YC

2. Change to your 3480/3/ folder.

Copy the lab files now...
cp /home/fac/gordon/p/3480/code/lab3/* .

Compile and run the program:
make
./lab3

Follow along on the big screen to begin this lab.
We will add one or more program features together.
You will then add some features yourself.

The following features are already listed in the program menu.

 . fill a disk (circle)
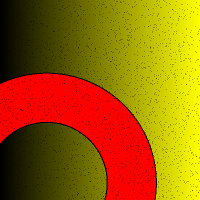
 . fill a ring
 . fill a rectangle
 . fill triangle using 3 half-spaces
 . fill triangle using odd-even method
 . calculate PI by inscribing a circle within a square
 . fill screen with checkerboard pattern
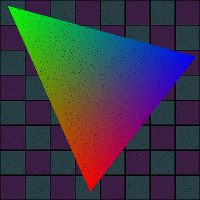
 . colored triangle using barycentric coordinates
 . fill triangle with a texture-map using barycentric coordinates

For the lab, you should try to do a few from step-3 and do step-4.
A few more features will be added for homework.

fill a disk
 . define g.center[2] and g.radius
 . find distance from point to center
 . compare distance to radius, and set the color

fill a ring
 . define g.center[2] and g.min_radius, g.max_radius
 . find distance from point to center
 . compare distance to min_radius and max_radius
 . set a color if between radii

fill a rectangle
 . define g.center[2], g.width, g.height
 . find horizontal distance from point to center
 . find vertical distance from point to center
 . compare distances to width and height
 . set a color if within

calculate PI
 . define your window size to be square in shape
 . define a circle that inscribes the square
 . start filling with pixels
 . keep a count of all pixels
 . keep a count of pixels inside the circle
 . pi = 4.0 * circle_pixels / all_pixels
 . at intervals, display pi on your console with printf
 . link

fill window with a checkerboard texture (procedural texture)
 . define a width and height of each checkerboard tile
 . start filling with pixels
 . check each pixel to see if it is on a white or black tile
 . try to do the calculation yourself
 . you may do some research if stuck

   try this...
      1 - divide pixel x by width
      2 - check if even/odd
      3 - divide pixel y by height
      4 - check if even/odd
      5 - are they the same or different?
      6 - set the color

Fill a triangle using 3 half spaces method.



space-1
space-2
space-3
combined







Notice how 3 spaces overlap to form a triangle in the middle.



Here is the process...

1. Build a vector from triangle vertex 0 to 1
   (subtract vertex 0 from vertex 1)
   name it v0

2. Build a vector perpendicular to v0
   name it v1

3. Build a vector from triangle vertex 0 to your point
   name it v2

4. Find the dot-product of v1, v2
   name it dot

5. Add the sign of dot to a sum (negative 1 or positive 1)

6. Repeat from step 1 for the two other triangle sides

7. If the absolute-value of sum is 3,
                 the point is inside the triangle.

This is an optional exercise in pseudocode conversion.

The pseudocode below fills a triangle using Odd-Even rule.

Determine if point at x, y is inside a triangle.
Use a horizontal line from (x,y) to (infinity,y).
Does line intersect any triangle sides?

notes: vert is a triangle_vertex from g.tri[3]
       a <-- b  means assign b to a

Use the pseudocode below to make this work.

set pixel color to blue
n <-- 0
i <-- 0
while (i < 3) do
    p0 <-- i
    p1 <-- (i+1) mod 3
    ydiff <-- (vert[p1][1] - vert[p0][1])
    if ydiff < 0 then
        SWAP p0 and p1
    end-if
    if y >= vert[p0][1] and y < vert[p1][1] then
        ydiff <-- (vert[p1][1] - vert[p0][1])
        xdiff <-- (vert[p1][0] - vert[p0][0])
        if xdiff not 0 then
            //slope = rise/run
            slope <-- ydiff/xdiff
            //x intersect is difference in y divided by the slope
            xintersect <-- (y - vert[p1][1]) / slope
            if (xintersect + vert[p1][0]) ≥ x then
                increment n
            end-if
        end-if
    end-if
    i <-- i+1
end-do
//odd number indicates inside
if n is odd then
    set pixel color to yellow
end-if
drawPoint(x,y);

--end of pseudocode--

Fill a triangle using barycentric coordinates.

You will probably need to write functions such as...

Flt getLength(Vec p1, Vec p2);
Flt getTriangleArea(Vec p1, Vec p2, Vec p3);
bool getBarycentric(Vec tri[3], int x, int y, Flt *u, Flt *v);

Use the u, v, w components to derive the color of each pixel
in the triangle.

Your triangle will be shaded like this...

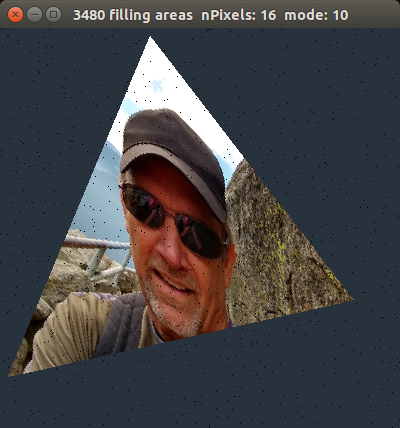
Fill a triangle with your picture from lab-1.
(or other image)

Bring in the Image class from your lab1.cpp.

Use barycentric coordinates of each pixel generated to get a color
from your Image data stream.

  1. use 3-half spaces to determine inside triangle
  2. generate barycentric coordinates for the pixel
  3. use u,v,w to scale each of the 3 (x,y) coordinates on your image.
  4. the sum of the scaled values will be the location of your color.
  5. go get the rgb color from the data stream.

sample image...


Extra effort:
Randomly generate all triangle vertices, but your triangle must
occupy at least 1/3 of the window area.

This gives you a bigger triangle to see your picture.

Fill a parallelogram with your picture from lab-1.
(or other image)

1. Generate a random triangle as before.
2. Add a 4th point to form a second triangle. (triangle mesh)
3. The triangles together should form a perfect parallelogram.
4. Map your entire image to the parallelogram.

sample image...

Lab-3 images from a previous student are below.
Cloose one or more images and try to duplicate them.
Make new menu items that will display your art.