CMPS 3120 Algorithm Analysis
Dynamic Programming
The change-making problem addresses the question of finding the minimum number of coins (of certain denominations) that add up to a given amount of money.
Given unlimited amounts of coins of denominations d1 > … > dm , give change for amount n with the least number of coins.
Abnormal coin change problem:
-
d1 = 25c, d2 = 11c, d3 =5c, d4 = 1c, and n = 15c
-
d1 = 25c, d2 = 11c, d3 =5c, d4 = 1c, and n = 1231c
My personal "magic spell" for Dynamic Programming:
Who am I? Where did I come from? Where am I going?
- Figure out the " Optimality Equation(s) "
- Find out the "Starting Value(s)"
- Set up a " Array / Matrix / Table ......"
- Back-tracking if needed
Row of coins picking problem: There is a row of n coins whose values are some positive integers c1,c2,...,cn, not necessarily distinct. The goal is to pick up the maximum amount of money subject to the constraint that no two coins adjacent in the initial row can be picked up.
- 3, 7, 4, 6, 8, 2. What is the best selection?
- 3, 7, 4, 6, 8, 2, 3, 8, 24, 18, 10, 19, 22, 14, 35, 12, 23. What is the best selection?
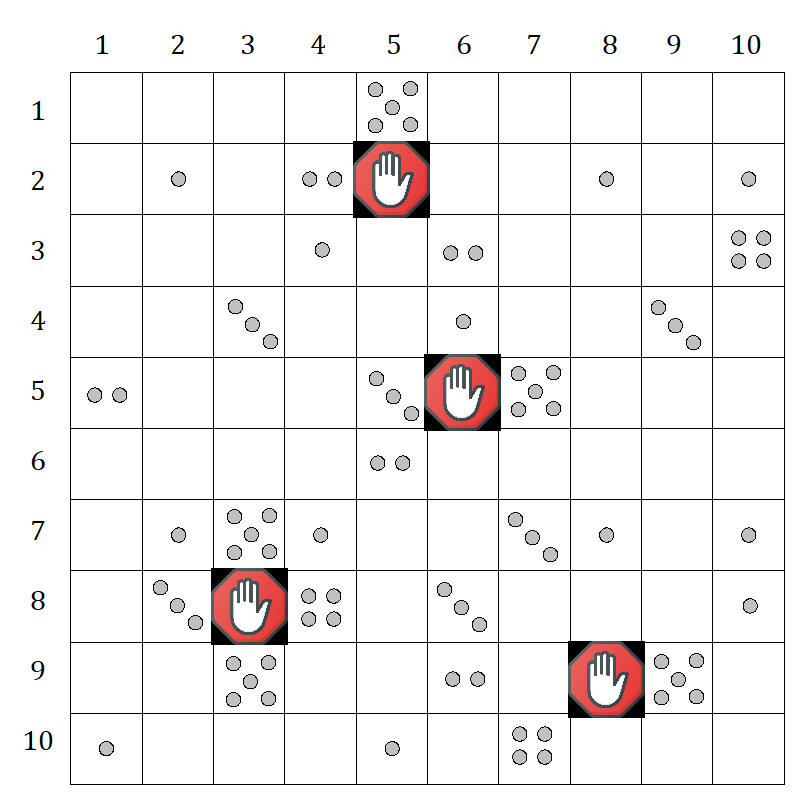
Robot Collect Coin problem: Several coins are placed in cells of an n×m board. A robot, located in the upper left cell of the board, needs to collect as many of the coins as possible and bring them to the bottom right cell. On each step, the robot can move either one cell to the right or one cell down from its current location.
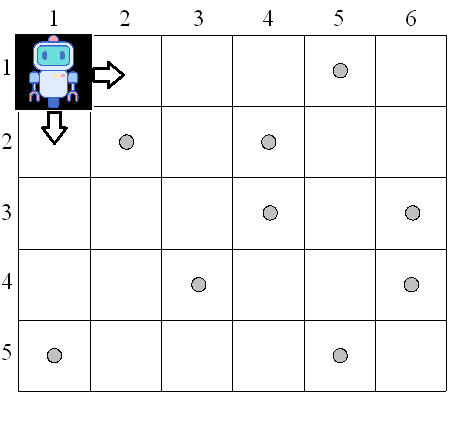
Can you update your algorithm if there are more than one coin in different cells?

Can you update your algorithm if there are some blocks in some of the cells?
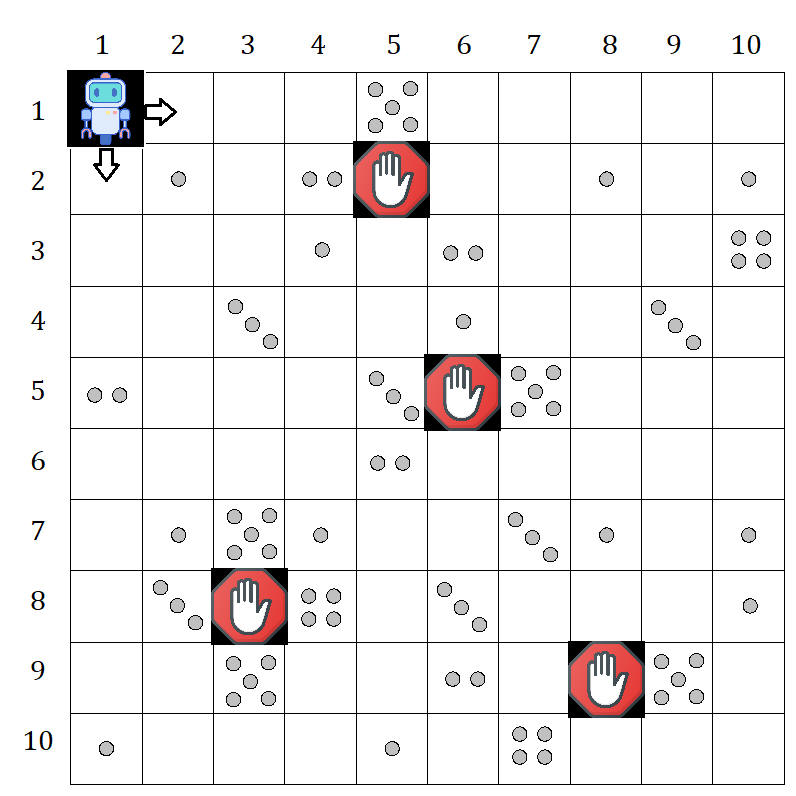
Can you update your algorithm if the robot can start from any cell?
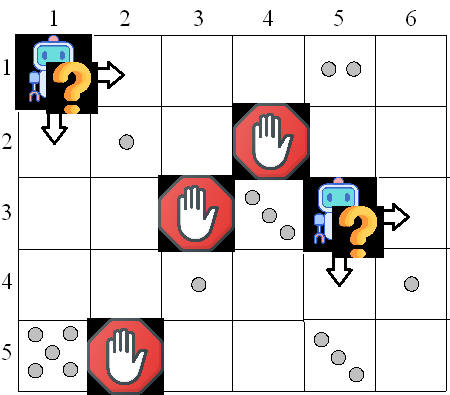
Can you update your algorithm if robot can start
from any cell
and you can choose the robot moving combination (right+down /
left+down / right+up / left+down)?