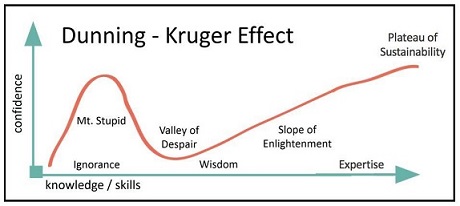
CMPS 3120 Algorithm Analysis
Introduction
=====>!!!Do not use any "magic function" in this class!!!<=====

=====>!!!No "class" in this class!!!<=====
Greatest Common Divisor problem: Find the largest integer that is a divisor of all the given numbers. Online GCD Calculator link
To be more specific: Find gcd(m,n), the greatest common divisor of two nonnegative, not both zero integers m and n.
What is included in this class
Least Common Multiple problem: LCM is also referred to as the Lowest Common Multiple (LCM) and Least Common Denominator (LCD) . For two integers a and b, denoted LCM(a,b), the LCM is the smallest integer that is evenly divisible by both a and b. Online LCM Calculator link

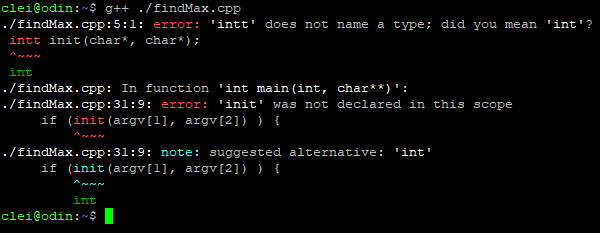
Please design an algorithm to find out the max number of the given array.
Is your algorithm correct? Prove that to me!
-
Oh, no~~~ It is NOT correct, what shall I do?
-
YES~~~ It is CORRECT!!!
![]()
-
See~~~ Check the output of the test case / Check the test case with the Pseudocode.
IT IS CORRECT!!!
Input test case: [13, 4, 24, 7]
Output: 24
|
-
This time, IT IS CORRECT~~~ What do you say for now!!!
Input test case: [13, 4, 24, 7]
Output: 24
Input test case: [-13, -4, -24, -7]
Output: -4
|
-
Examples / Test cases can only be used to prove that an implemented algorithm is not correct, by discovering inputs where the output is unexpected. However, it cannot prove that an algorithm is correct. [ref]
| Example Algorithm | Explanation | |
| Pseudocode |
MERGE-SORT A[1 . . n]
1.If
n
= 1,
done.
2.Recursively sort
A[
1 . .
én/2ù
]
and
A[
én/2ù+1
. .
n
]
.
3.“Merge”
the
2
sorted lists.
|
White the pseudocode to "high-level" discribe the algorithm |
| Prove the Correctness |
Proof by induction:
1.Base case: if n = 1, the algorithm will return the
correct answer because
A[1..1]
is already sorted.
2.Inductive hypothesis: assume that the algorithm correctly
sorts
A[1.. én/2ù ] and A[én/2ù+1..n].
3.Step: if
A[1..
én/2ù
]
and
A[én/2ù+1..n]
are both correctly sorted, the whole array
A[1..
én/2ù
]
and
A[én/2ù+1..n]
is sorted after merging.
|
Mathematical proof: for each input it produces the expected output |
| Time Efficiency Analysis |
T(n)
=Q(1)
if
n
= 1; |
A measure of amount of time(how do you define "time"? ) for an algorithm to execute |
| Space Efficiency Analysis | ...... | ...... |
Sum of N numbers / Gauss’ Trick
(link):
The
story goes that, in school, at the age of 8,
Carl Friedrich Gauss was able to add up the first 100
numbers extremely quickly. I like to think of the teacher as
having used this trick many times to keep the class busy for
long periods while he took a snooze. He knew that he was in for
a long quiet period as the class slaved away. Even if one of
them got an answer, the teacher could ask them to check it to
take up more time. But he hadn’t bargained on this precocious 8
year old.
In a flash Gauss came out with 5050. But not only could he
calculate the sum of the first 100 numbers that quickly, he
could also justify the correctness of his answer.
Check the following 3 algorithms, which one is the fastest?
def sum1(n) :
total = 0
for i in range(n+1):
total += i
return total
def sum2(n) :
if n == 1:
return 1
else:
return sum2(n-1)+n
def sum3(n) :
return n*(1+n)/2