(Dis)Similarity / Corrolation
(Dis)Similarity calculation also
quantifies how (different) similar two data points are, but the
term "(dis)similarity" often refers to a broader concept that
includes both distance measures and other metrics that focus on
different kinds of disparities between points. It is used more
generally in clustering, classification, or other unsupervised
learning algorithms to describe how "(un)like" two points are.
While distance measures are always non-negative, (dis)similarity
can sometimes allow for asymmetric calculations
(i.e., (dis)similarity between A and B is not necessarily the
same as between B and A).
In some cases, (dis)similarity can refer to any kind of
calculation that reflects how (different) similar two objects
are.
What methods can we use?
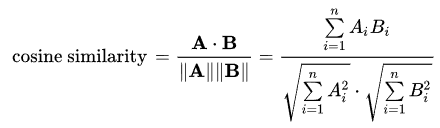
![]()
Pearson Correlation Coefficient
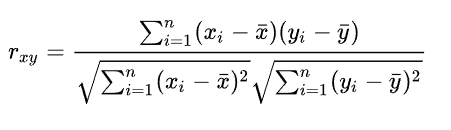
The advantage of the Pearson Coefficient over the Euclidean Distance is that it is more robust against data that isn't normalized.
The value range is from -1 to 1 .
Spearman's Rank Correlation Coefficient
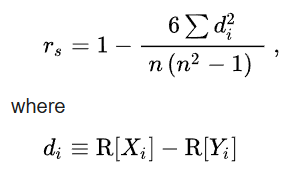
di is the difference between
the two ranks of each observation,
n is the number of observations.
In simple words, we first rank all data, then calculate the Pearson Correlation Coefficient based on ranking.
Note, unlike Pearson’s correlation,
there is no requirement of normality and hence it
is a nonparametric statistic.
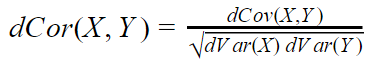
Distance correlation measures the dependence between two random variables, regardless of their types. It can be used to detect any kind of dependence between variables (linear or nonlinear) and works well with mixed data types.
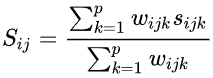
Gower's distance between two mixed-type
objects is a similarity measure that can handle different types
of data within the same dataset and is particularly useful in
cluster analysis or other multivariate statistical techniques.
Data can be binary, ordinal, or continuous variables. It works
by normalizing the differences between each pair of variables
and then computing a weighted average of these differences.
The value is between 0 and 1 with smaller values indicating higher similarity.
Kendall Rank Correlation Coefficient
![]()
The Kendall rank correlation
coefficient, commonly referred to as Kendall's τ coefficient, is
a statistic used to measure the ordinal association between two
measured quantities.
It is a measure of rank correlation: the similarity of the
orderings of the data when ranked by each of the quantities.