Data Science
Polynomial Regression
Polynomial regression is a form of regression analysis in
which the relationship between the independent variable x and
the dependent variable y is modeled as an nth degree polynomial
in x.
Polynomial regression fits a nonlinear relationship between the
value of x and the corresponding conditional mean of y, denoted
E(y |x).
Although polynomial regression fits a nonlinear model to the data, as a statistical estimation problem it is linear, in the sense that the regression function E(y|x) is linear in the unknown parameters that are estimated from the data. For this reason, polynomial regression is considered to be a special case of multiple linear regression.
We can model the expected value of y as an nth degree
polynomial, yielding the general polynomial regression model
![]()
Polynomial regression models are usually fit using the method
of
least squares. The least-squares method minimizes the
variance of the unbiased estimators of the coefficients.
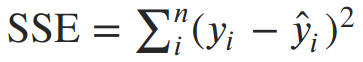
Although it can model non-linear relationships between variables, polynomial regression is considered a type of linear regression because the model itself is linear in its parameters, meaning the coefficients are linear even when the polynomial degree is high; therefore, it is technically classified as "linear" in the statistical sense.
Here is one day's temperature data of our campus.

Please try to fit a polynomial regression function to best estimate the temperature.
What is the SSE of your model?