Measurements
Given two data points, we can calculate
a value to represent the distance/similarity/dissimilarity
between those two data points.
Given a group of data,
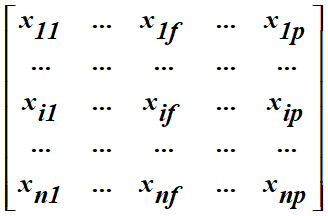
There are n data
points and each data point has p
dimensions.
We can calculate a
n by n matrix to
represent the distance/similarity/dissimilarity of the entire
dataset.
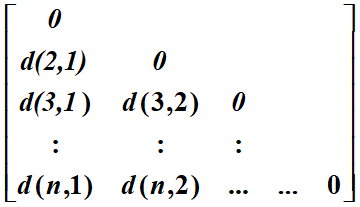
Here are some sample questions.
Distance measures quantify the degree of
separation or distance between two data points in a specific
metric space.
The focus here is on determining how far apart two points are in
terms of their coordinates, features, or representations.
Distance measures are always non-negative and are usually
symmetric (i.e., the distance from point A to point B is the
same as the distance from point B to point A).
Distance Measures are
typically associated with geometrical or numerical
representations,
often used in vector spaces and metrics.
Euclidean distance
Standardized Euclidean distance
Manhattan distance
Chebyshev distance
Minkowski distance
Hamming distance
Jaccard distance
(Dis)Similarity calculation also
quantifies how (different) similar two data points are, but the
term "(dis)similarity" often refers to a broader concept that
includes both distance measures and other metrics that focus on
different kinds of disparities between points. It is used more
generally in clustering, classification, or other unsupervised
learning algorithms to describe how "(un)like" two points are.
While distance measures are always non-negative, (dis)similarity
can sometimes allow for asymmetric calculations
(i.e., (dis)similarity between A and B is not necessarily the
same as between B and A).
In some cases, (dis)similarity can refer to any kind of
calculation that reflects how (different) similar two objects
are.
(Dis)Similarity Calculation is more general concept, which could involve distance measures, but also includes non-geometric measures (including those for categorical data or set-based data), reflecting the difference between data points in a broader sense.
Cosine Similarity
Jaccard Similarity
Pearson Correlation Coefficient
Spearman’s Rank Correlation
Distance Correlation
Gower's Distance
Kendall Rank Correlation Coefficient